by Patrick Mayr
The most used DeFi lending protocols today offer variable rates for both lenders and borrowers. While variable rate lending is an important pillar of DeFi, it’s a product that isn’t suitable for everyone. Interest rate volatility makes it difficult to plan for the future, make investment decisions and hedge risk when borrowing and lending.
In traditional financial markets, fixed rate lending markets account for the vast majority of lending volume as they provide predictability and minimize risks for market participants. In DeFi, fixed rate lending markets only account for a fraction of the total lending market. The top 3 variable rate protocols - Aave, Compound and MakerDAO - have a cumulative TVL of around $13.6B. The 3 largest fixed rate protocols - Notional, Pendle and Yield - have a cumulative TVL of around $80M.
This post examines the designs of 3 protocols that create fixed rates in DeFi through different approaches:
- Notional - zero coupon bonds
- Element - yield stripping + zero coupon bonds
- Voltz - interest rate swaps
We compare and contrast the approaches, talk about the challenges facing the protocols, and offer some thoughts on what can catalyse growth in the category.
Notional Finance
Notional relies on a construct that mimics zero coupon bonds to achieve fixed rates. Yield is a protocol with a similar design.
First, let’s briefly explain the concept of zero coupon bonds. Per Investopedia, “a zero coupon bond is a debt security that does not pay interest but instead trades at a deep discount, rendering a profit at maturity, when the bond is redeemed for its full face value.”
A zero coupon bond’s price is calculated by the following formula:
P = M ÷ (1 +r )^n
Where, P is the price of the bond, M the value of the underlying at maturity, r the annual interest rate, and n the number of years to maturity.
Let’s run through a quick example. Let’s assume a bond with a face value of $100 is sold for $95. Assuming a time to maturity of 1 year, the investor, assuming the loan is repaid, makes a $5 return. This translates to an implied interest rate, or rate of return, of 5% which is calculated as follows:
95 = 100 ÷ (1+r)^1
Solving for r gets you:
r = 0.05 or 5%
Coming back to Notional, the core construct in Notional is a set of synthetic assets collectively known as fCash. fCash are tokens created in pairs, positive and negative, such that the sum of their values always equals 0. For instance, a positive 105 fCash token would be minted together with a negative 105 fCash token. A positive fCash token is an asset that represents a claim on a cash flow at a given maturity. A negative fCash token is a liability that requires its holder to pay a certain amount at a given maturity. Notional works with set maturities that each participant in the network needs to choose from.
fCash tokens are denominated in a base asset and settled in a yield generating version of that same base asset. For example, if fCash is denominated in a base asset like DAI, it is settled in cDAI. Settlement in interest bearing assets like cTokens optimizes the capital efficiency of the system as users transact in interest bearing assets that continue to generate yield irrespective of their utilization on Notional.
For example, the holder of positive 105 Dec. 1 2021 fDAI will receive 105 DAI worth of cDAI on December 1, 2021. The holder of negative 105 Dec. 1, 2021 fDAI will need to pay 105 DAI worth of cDAI on December 1, 2021.
Example
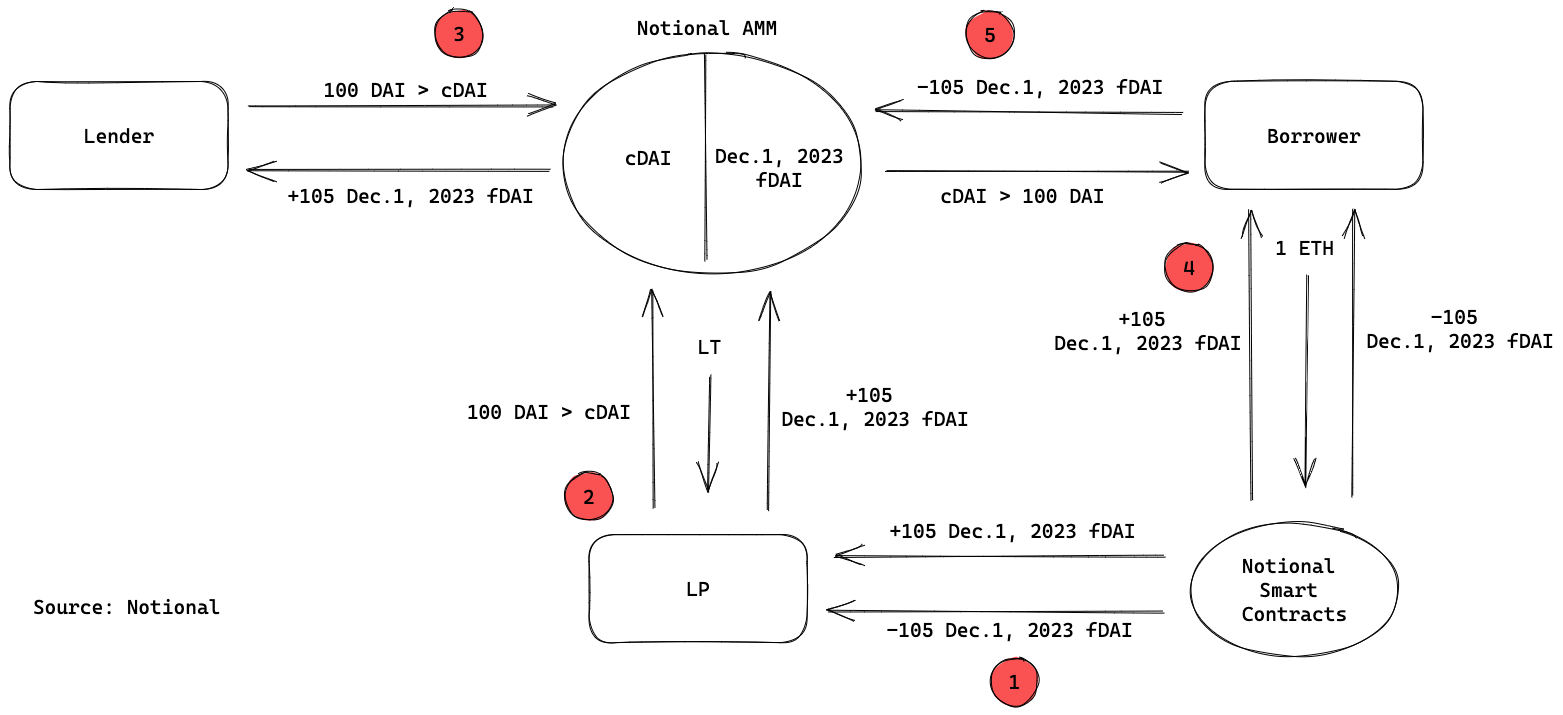
Let’s walk through a specific example to better understand how Notional works. We’ll refer to the illustration above, using a December 1, 2023 maturity. The participants in the Notional system are lenders, borrowers and liquidity providers (LPs).
- LPs are required by Notional to provide liquidity that lenders and borrowers trade against. In this case an LP wants to provide 100 DAI worth of cDAI in liquidity, so he mints a pair - positive and negative - of 105 Dec.1, 2023 fDAI tokens. In step 3 we’ll explain why 100 DAI worth of cDAI enables the LP to mint a pair of 105 fDAI tokens.
- The positive fCash token and cDAI are deposited in the Notional Automated Market Maker (AMM). In exchange, the LP receives Liquidity Tokens (LT) that reflect his position in the AMM. LPs earn fees every time a lender or borrower trades between cDAI and fDAI on the AMM.
- A lender decides to lend 100 DAI for a fixed rate. He first converts 100 DAI into cDAI that he deposits into the Notional AMM. In exchange he receives 105 fDAI. The cDAI / fDAI exchange rate is the fixed rate, which is determined algorithmically by the AMM. Here is where the zero-coupon bond effect plays out: the lender initially sends 100 DAI into the AMM and in return receives 105 Dec.1, 2023 fDAI that can be redeemed for 105 DAI at maturity. The $5 difference between what the lender initially lends out and receives at maturity constitutes the fixed rate. The cDAI / fDAI exchange rate was also applied to the LP in step 1. Minting fDAI tokens and providing liquidity happens in the same step for LPs, but we’ve just broken it down here to explain what’s happening more clearly. Before the first LP deposits liquidity into an AMM pool for a specific maturity, the cDAI / fDAI exchange rate is initialized by the protocol. Afterwards, market forces set the rate.
- A borrower wants to take out a 100 DAI loan. In order to do so he mints a pair of 105 Dec.1, 2023 fDAI tokens collateralized with 1 ETH. The borrower, as opposed to the LP, needs to post collateral because he is taking out a loan. The collateral serves as protection in case of a default and can be liquidated to retain the system’s solvency.
- The borrower deposits the positive fDAI token into the AMM in exchange for cDAI. Now the borrower holds both cDAI (which can be converted to 100 DAI) and a negative 105 Dec.1, 2023 fDAI token that represents a future obligation to pay 105 DAI at maturity. The $5 difference between what the borrower initially borrows and needs to pay back at maturity constitutes the fixed rate. Minting fDAI and exchanging fDAI with DAI through the AMM happens in the same step for the borrower. In practice, minting fCash is abstracted away for all users as it’s simply Notional’s internal accounting mechanism.
Element Finance
Element combines yield stripping with a zero-coupon bond mechanism to create fixed rates. It is similar in design to other protocols such as Pendle, Swivel and APWine.
Yield stripping is a construct that allows users to split a yield generating asset into two separate assets at a specific maturity. For example, yvDAI (interest generating DAI on Yearn), can be split into a Principal Token (PT), which represents the value of the principal, and a Yield Token (YT), which represents the interest generated on the principal.
Once the tokens are split, the PTs can be traded against their underlying on the Element AMM. The PT / base token exchange rate constitutes the fixed rate. YTs can also be traded on Element. They don’t, however, play a role in the mechanism that creates fixed rates on Element.
Example
In this example we’ll start with the yield splitting component, which precedes any other activity on Element, and then dive into the fixed rate mechanism. Here, we’ve used a 1-year maturity. The participants in the Element system are fixed rate buyers, variable rate depositors and LPs.
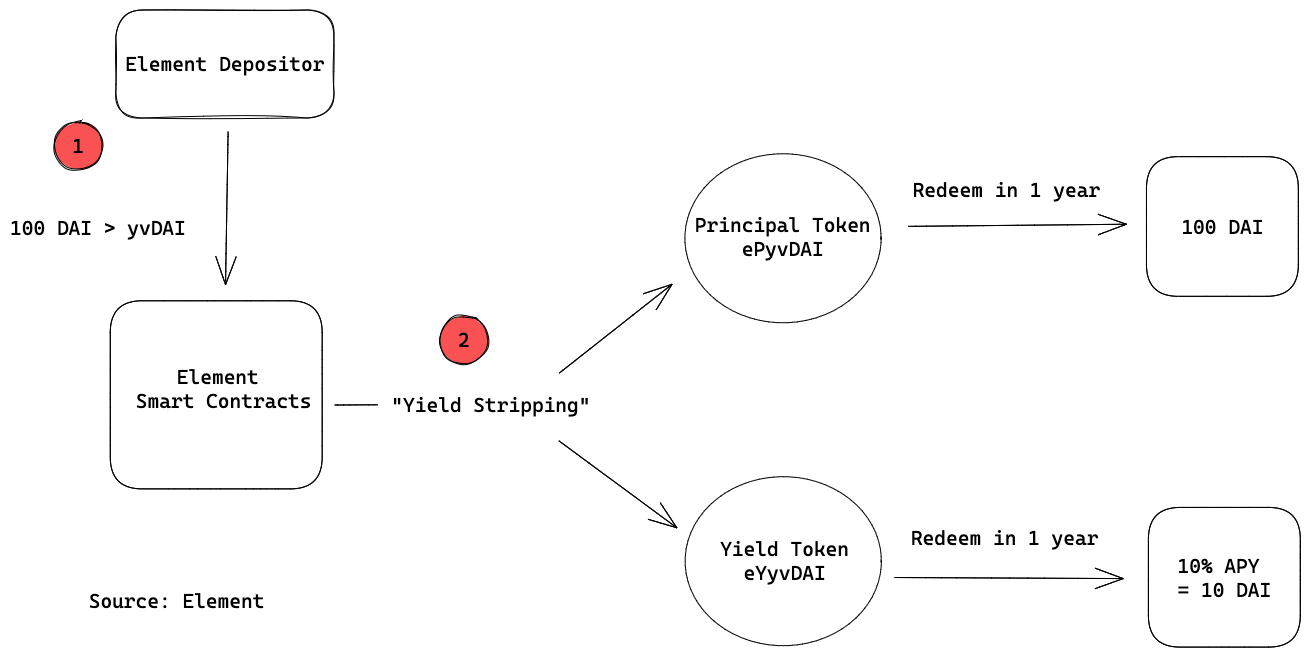
- A user deposits 100 DAI into a Yearn vault and receives 100 DAI worth of yvDAI in return. Yield generated from Yearn vaults is variable, but if we project an APY of 10% on the DAI in the vault, in 1 year yvDAI can be redeemed for 110 DAI. The user then sends the yvDAI to Element in order to split them into two separate assets for a 1-year maturity.
- The user receives newly minted PTs (ePyvDAI) and YTs (eYyvDAI). The PTs represent the principal sitting in the Yearn vault worth 100 DAI and the YTs represent the annual yield of 10% on the principal.
Now let’s dive into the mechanism that generates fixed rates. You’ll notice that this part is somewhat similar to Notional.
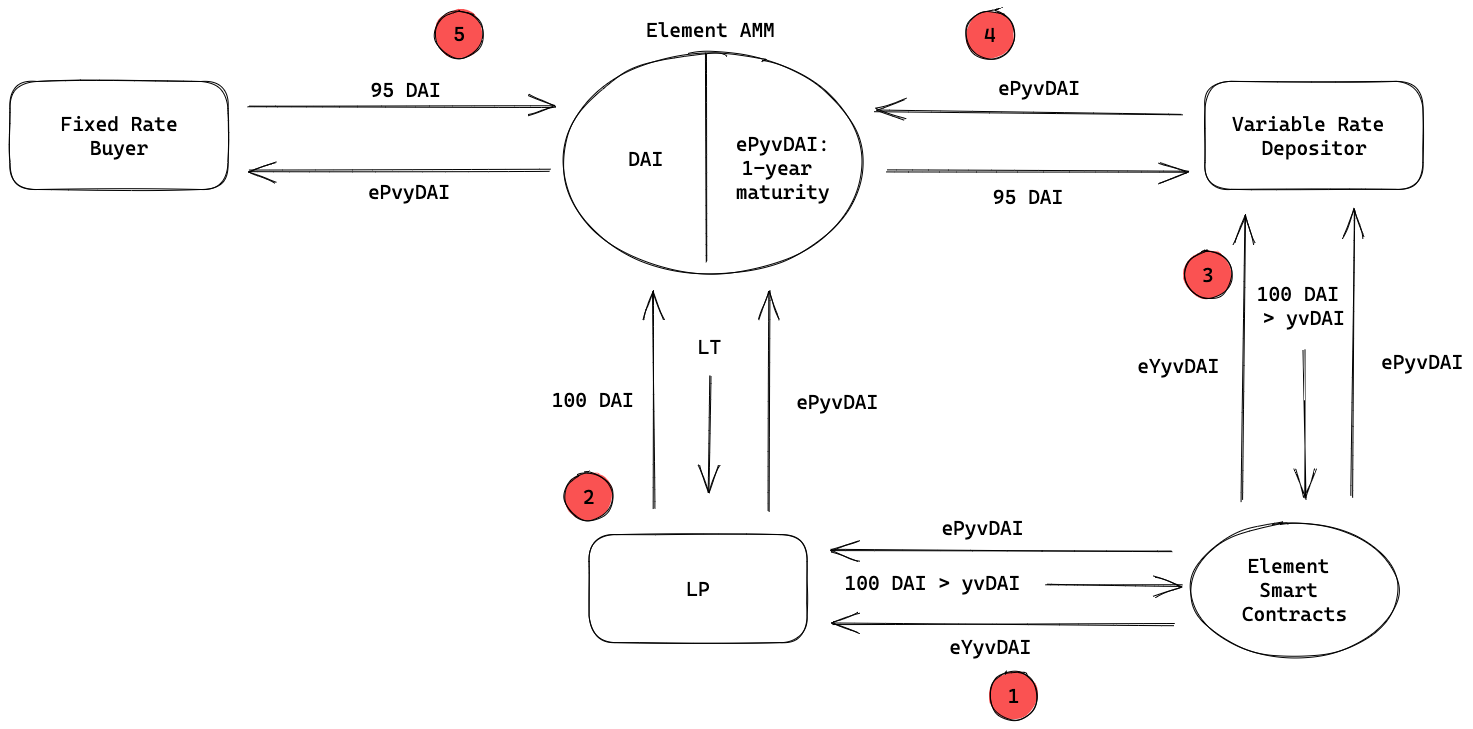
- Element requires LPs to provide liquidity for the system. In order to do so, LPs need to go through the yield stripping process shown above. In this example, an LP deposits 100 DAI worth of yvDAI to “yield strip” and receives the corresponding amount of ePyvDAI and eYyvDAI.
- The LP deposits 100 DAI and 100 DAI worth of ePyvDAI in the Element AMM and receives LTs in return. LPs earn fees every time a lender or borrower trades between ePyvDAI and DAI on the AMM.
- Another user also decides to yield strip 100 DAI worth of yvDAI and receives the corresponding amount of ePyvDAI and eYyvDAI in return.
- That user then decides to become a variable rate depositor and sells 100 DAI worth of ePyvDAI for 95 DAI on the Element AMM. The ePyvDAI / DAI exchange rate determined algorithmically by the AMM constitutes the fixed rate. In this case, the variable rate depositor sells ePyvDAI at a discount to its face value to access the DAI earlier. At maturity, the price of ePyvDAI converges to the price of DAI. There are many reasons to become a variable rate depositor. One particular reason can be that the user only values the variable yield that he thinks will go up, and as a result wants to increase his exposure to YTs. With the purchased DAI, the variable rate depositor can purchase more YT tokens on Element. The difference to Notional is that a variable rate depositor is not a “borrower” per say but a user that just sells their PT at a discount to their underlying asset. This means that they don’t have a future obligation to repay a loan.
- A fixed rate buyer purchases 100 DAI worth of ePyvDAI for 95 DAI. At maturity, the lender can redeem the ePyvDAI for 100 DAI, netting a $5 fixed rate of return.
Voltz
Voltz is an interest rates swap (IRS) protocol that allows fixed rate takers to trade variable rates for fixed rates, and for variable rate takers to trade fixed rates for variable rates.
Voltz uses a virtual AMM (vAMM) for price discovery. Unlike the Notional and Element AMMs, where assets are moved into a liquidity pool, Voltz utilizes the vAMM for price discovery while the management of users’ underlying assets is done through the margin engine.
Similar to Notional and Element, Voltz works with set maturities.
Example
The participants in the Voltz system are fixed rate takers, variable rate takers, and LPs.
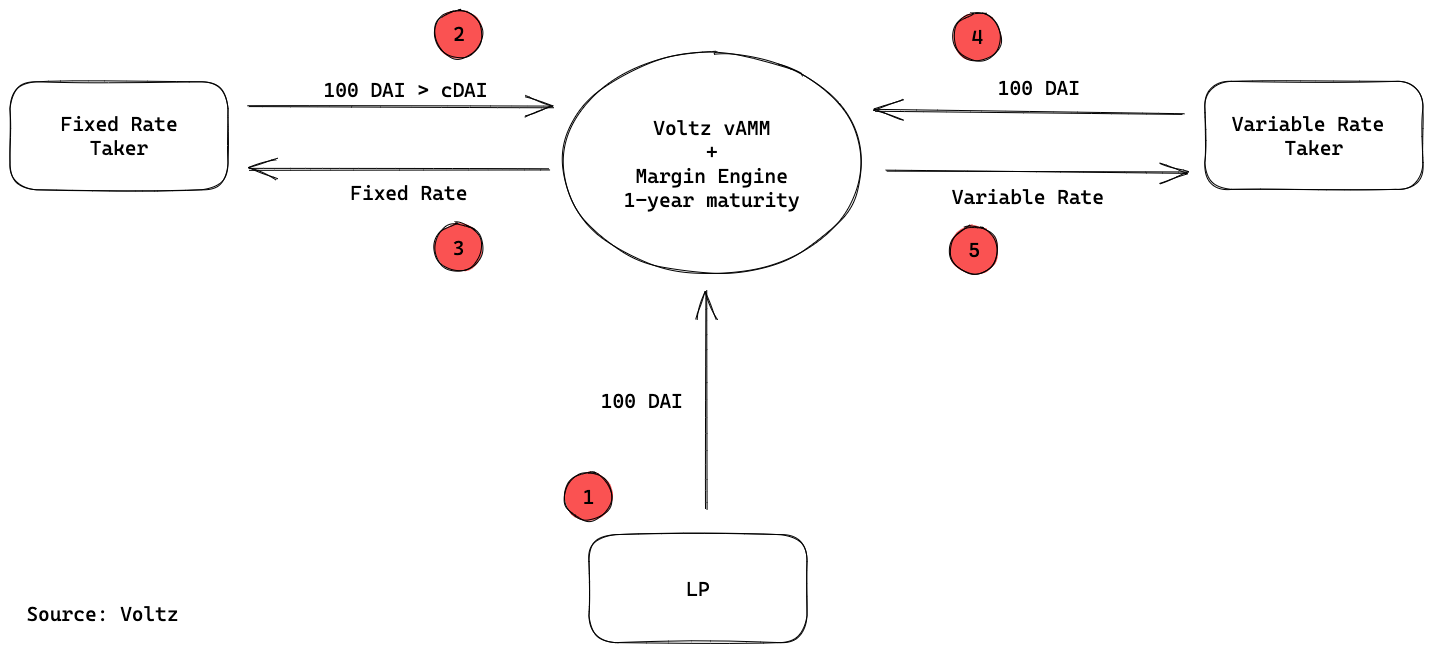
- Due to the fact that the vAMM is only used for pricing, and fixed and variable interest rates are made in the same underlying asset, LPs only need to provide liquidity with one asset. In this case the interest rates are denominated in DAI so the LP provides 100 DAI in liquidity.
- A fixed rate taker owns 100 DAI worth of cDAI which has a current variable rate of 5% APY on Compound. Instead of maintaining exposure to the variable rate, which may increase or decrease, the fixed rate taker opts for more certainty and decides to trade the variable interest rate for a fixed rate on Voltz. To do so he first sends cDAI to the Voltz margin engine that manages the assets.
- The fixed rate is determined by the vAMM. Let’s assume it’s 10%. At maturity in 1 year, the fixed rate taker would receive the 100 DAI worth plus the accrued interest. This is calculated as follows: Notional * (1+r)^(n ÷365) => 100 * (1+0.1)^1= 110 DAI
- A variable rate taker has 100 DAI. The current variable rate on cDAI is 5% and the fixed rate on Voltz is 10%. The variable rate taker thinks that the variable rate on Compound will increase to a rate that’s higher than the fixed rate on Voltz, so he wants additional exposure to it. He deposits 100 DAI in the Voltz margin engine. The 100 DAI will be used to make the fixed rate interest payments to the fixed rate taker. Variable rate takers will typically take a leverage on Voltz, but in this example we’ve omitted it for simplicity’s sake.
- The variable rate on Compound did end up jumping to 25% on Compound for the duration of maturity period. The variable rate taker earns the difference between the variable and fixed rates. At maturity he receives the following: 100*(1+(0.25-0.1)^1= 115 DAI. If the variable rate had been below the fixed rate, the variable rate taker would have lost money.
Comparing the protocols
Below is a comparison of the protocols using a DAI market as an example.
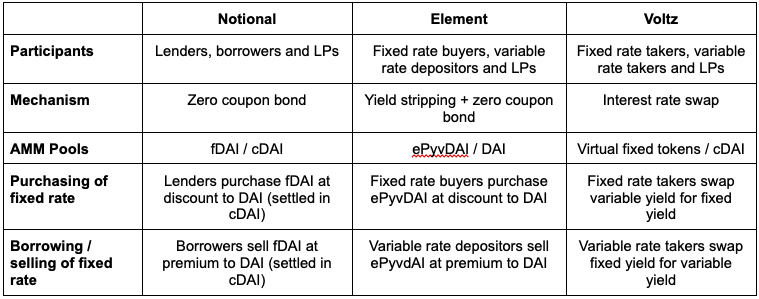
All the discussed protocols rely on an AMM to determine the fixed rates. In Notional and Element, the AMM holds and manages tokens that participants in the system trade against while Voltz leverages a vAMM that exclusively prices the fixed rate while token management and liquidations are handled through the margin engine.
Notional and Element both leverage a zero coupon bond mechanism. They create a synthetic, zero coupon bond-like instrument—fCash and PTs —that is traded against an underlying asset and that can be redeemed 1:1 for that asset at maturity. The exchange rate between the synthetic and underlying asset at the time of the trade, determined by the AMM, constitutes the fixed rate.
Notional is most clearly structured as a lending market that offers lenders and borrowers a direct alternative to variable rate lending markets such as Compound or Aave. On Element, fixed rate buyers are akin to lenders but variable rate buyers are not borrowers as they simply trade between two assets and don’t have any future obligation to repay a loan. Voltz is an interest rate derivatives market which is the furthest removed from lending markets, as it offers participants with interest rate exposure to hedge their existing positions.
Challenges and outlook
When looking for reasons as to why DeFi fixed rates haven’t generated significant traction yet, I’d point to 3 main ones:
- Fragmented liquidity
- Little-to-no flexibility to determine terms
- Not fit for institutions
The little liquidity there is in these protocols is fragmented across different maturity pools in the AMMs, which makes it more difficult for participants to execute trades and receive good rates.
Users have little flexibility to determine terms. While interest rates set by AMMs can work for a certain set of users, others require more flexibility to negotiate terms directly with their counterparty in a peer-to-peer fashion. This also applies to duration, which is probably the most important point that lacks flexibility in the current designs. It will be interesting to see if some of the new developments that make variable rate lending protocols more efficient and flexible, such as the peer-to-peer markets that Morpho have pioneered, also get applied to fixed rate lending.
Institutions would be a great fit for fixed rate protocols. The protocols are complex and require a greater degree of sophistication from users than variable rate protocols. Fixed rates also provide institutions with more certainty that they require. The protocols are, however, not yet ready to service institutions. KYC / AML and permissioned pools would assuage some of the fears institutions likely have at the moment.
Special thanks to Brett Sun and Luca Prosperi for their thoughts and comments on this post.